About Me

I am a post-doctoral researcher at the Max-Planck Institute for Mathematics in the Sciences in Leipzig, supervised by Guido Montufar and Bernd Sturmfels. I completed my PhD in Mathematics at TU Berlin under the supervision of Martin Skutella. My research focuses on neural networks theory using polyhedral geometry, combinatorics, computational complexity and topology. I previously earned a B.Sc. in Mathematics and Computer Science and an M.Sc. in Mathematics from the University of Greifswald
News
- Talk at the annual meeting of the SPP Theoretical Foundations of Deep Learning about the project combinatorial and implicit approaches to deep learning.
- Our paper Depths-Bounds for Neural Networks via the Braid Arrangement was accepted as oral at NeurIPS 2025.
- The defense of my PhD thesis Expressivity and Complexity of ReLU Neural Networks was on October 2nd. Here are the slides.
Preprints
Parameterized Hardness of Zonotope Containment and Neural Network Verification
On the Expressivity of Sparse Maxout Networks
Publications
Depth-Bounds for Neural Networks via the Braid Arrangement
(Oral) Conference on Neural Information Processing Systems (NeurIPS) 2025
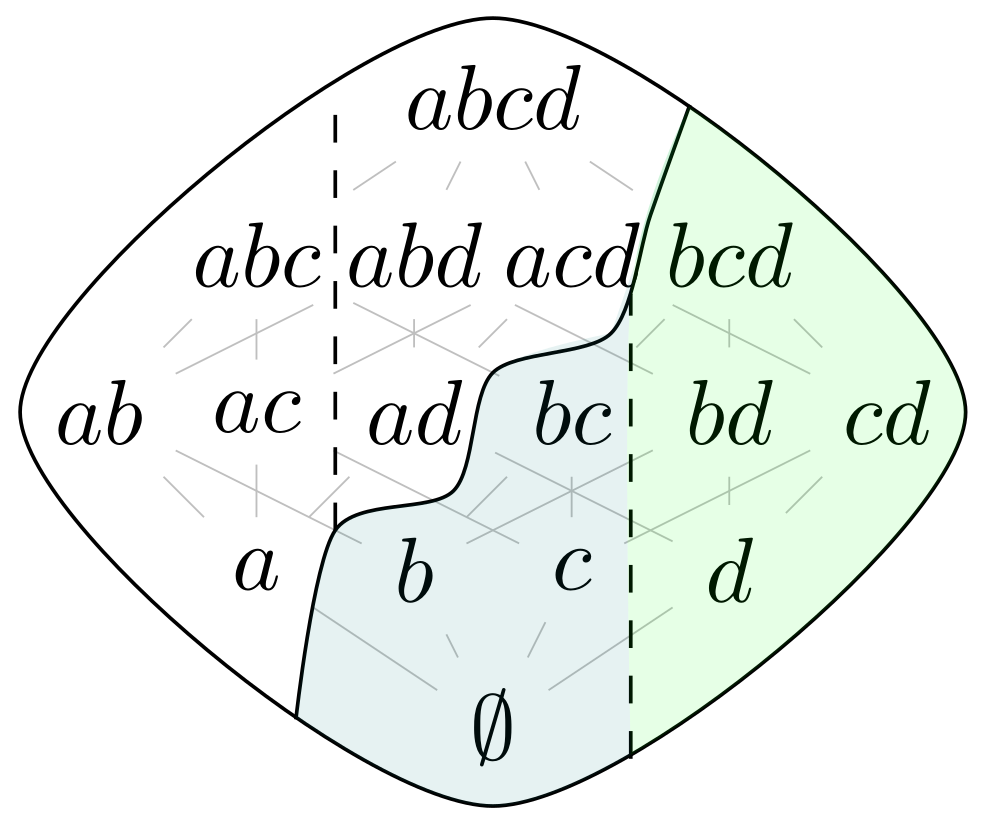
Complexity of Deciding Injectivity and Verification of ReLU Neural Networks
Conference on Learning Theory (COLT) 2025
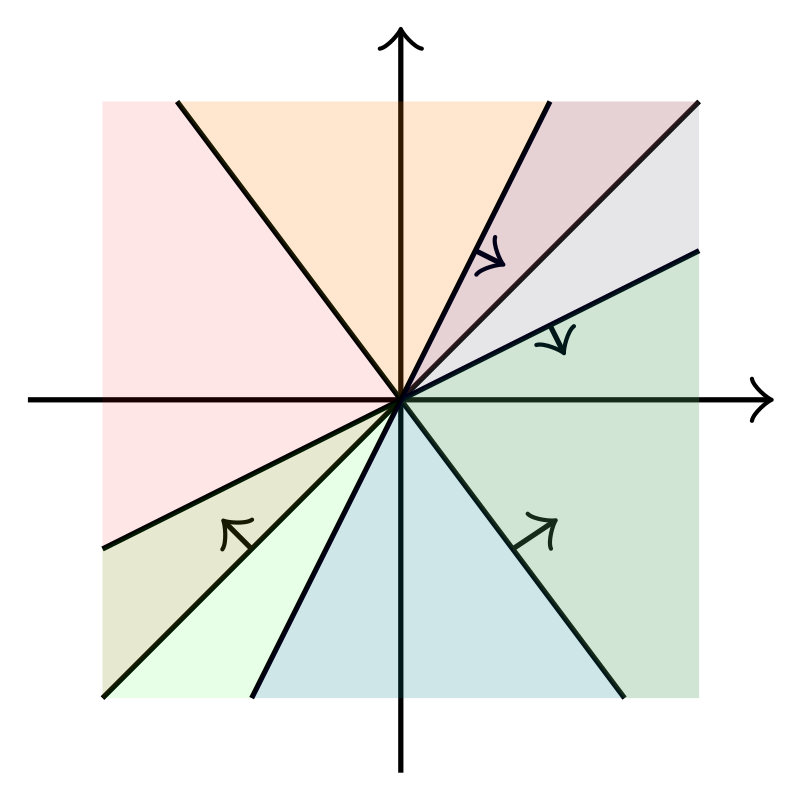
Decomposition Polyhedra of Piecewise Linear Functions
(Spotlight) International Conference on Learning Representations (ICLR) 2025
Conference Version | Preprint | Video | Poster | Slides
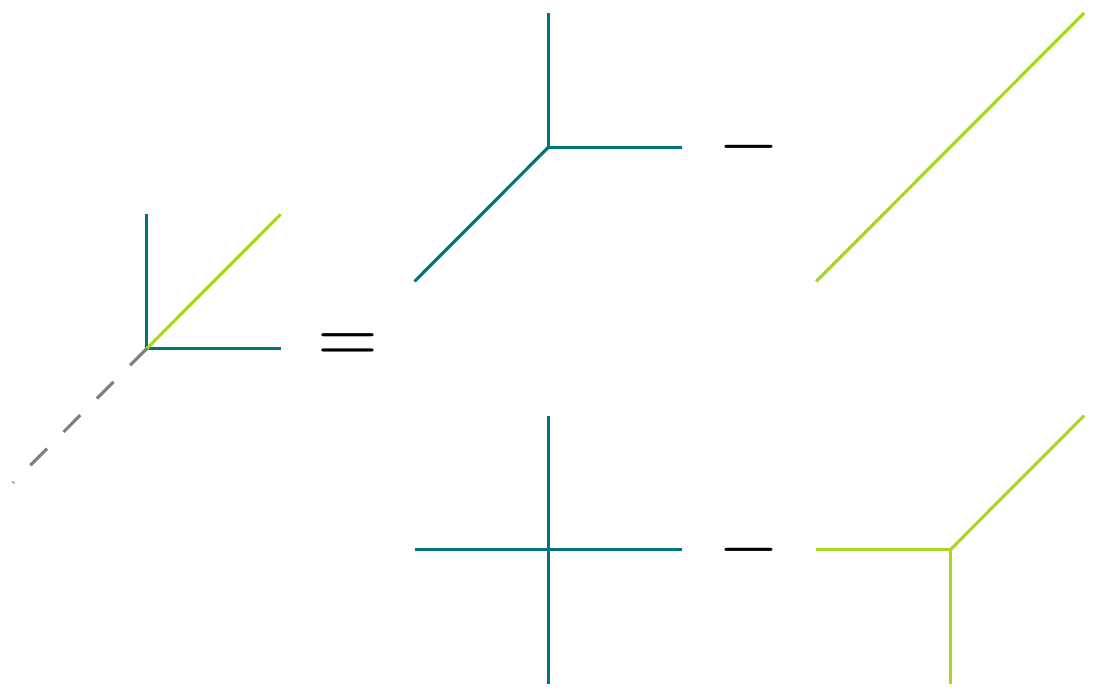
Topological Expressivity of ReLU Neural Networks
Conference on Learning Theory (COLT) 2024